David Letterman goes on vacation and decides to drop a watermelon off the edge of the Grand Canyon. The melon falls, starting from rest, and travels a distance, d, in t seconds. How much farther will the melon travel if allowed to fall for 2t seconds, again starting from rest?
Chester has placed three rocks on one of his big sister Erin's favorite albums to watch them spin and hopefully fly off. All the rocks have a mass of 10 g. Chester has placed rocks at 5 cm, 10 cm, and 15 cm away from the center of the album. The coefficient of static friction between the rocks and the record is 0.1.
a) If the record is rotating at 33 rpm, which rock(s) will fly off the album? (10 points) (Circle one)
b) Chester gets excited and turns up the speed on the turntable to 78 rpm. Which rocks will fly off now? (5 points) (Circle one)
Flying Fred Zucchini has a trampoline act. He has a mass of 75 kg. His trampoline is a (massless) platform on a spring with a spring constant of 8,000 N/m. Fred hits the trampoline moving downward at 5 m/s. He then compresses the spring a distance of 0.45 meters, but he has not yet come to rest.
a) How much work is done on Fred by the force of gravity when the spring is compressed 0.45 meters? (6 points)
b) How much work is done on Fred by the spring as it is compressed 0.45 meters? (6 points)
c) What is Fred's downward speed once the spring has been compressed 0.45 meters? (8 points)
Calvin is planning to throw a water balloon at his dad's car when he comes home from work. With the help of his faithful sidekick, Hobbes, he has climbed up to the top of a tree. He throws the water balloon at an angle of 40! above the horizontal, with an initial velocity of 8 m/s. The water balloon starts from a height 12 meters above the ground.
a) How long after he throws it will Calvin's water balloon hit the ground? (7points)
b) What is the horizontal range of Calvin's water balloon? (6 points)
c) Hobbes is standing at the base of the tree. He wants to throw his own water balloon. He will launch it at the same time as Calvin, but at an angle of 60! with respect to the horizontal. With what initial speed must he throw it in order for his balloon to hit the ground at the same time as Calvin's? (He doesn't care if his balloon does not land in the same place as Calvin's) (7 points)
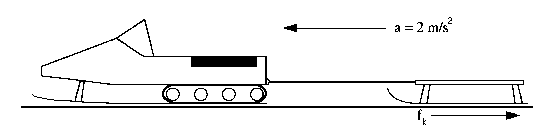
A snowmobile is pulling a 15 kg sled along a horizontal skiing trail with a stretchable bungy cord. The bungy cord stays parallel to the ground and behaves exactly like a spring with a spring constant, k, of 50 N/m. The coefficient of kinetic friction between the sled and the snow is 0.15. The sled and snowmobile are accelerating at 2 meters per second squared, and remain separated by a fixed distance.

a) Calculate the tension in the bungy cord. (8 points) (Circle one)
b) Calculate how far the cord is stretched from its relaxed position. (7points) (Circle one)
Janet sits on a cafeteria tray and slides down a very icy hill in the Arb (my note: sliding down hills in the arboretum (the "Arb") was a very common passtime on snowy Friday nights in Ann Arbor), starting from rest. Together, Janet and her tray have a mass of 50 kg. The hill is 80 meters long, and makes an angle of 30 degrees with the horizontal surface below. At the end of the hill, there is a smooth transition to the flat surface. All surfaces have a coefficient of kinetic friction of 0.1.
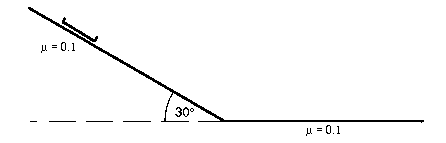
a) Draw a free body diagram showing all forces acting on the combination of Janet and her tray when she is sliding down the hill. (5 points)
b) Calculate Janet's acceleration as she slides down the hill. (5 points)
c) What is Janet's speed at the bottom of the slope? (5 points)
d) What is Janet's deceleration when she is on the horizontal surface at the end of the hill? (5 points)
e) How far will Janet slide on the horizontal surface before coming to rest?
(5 points)
Look at my thoughts on the exam.